
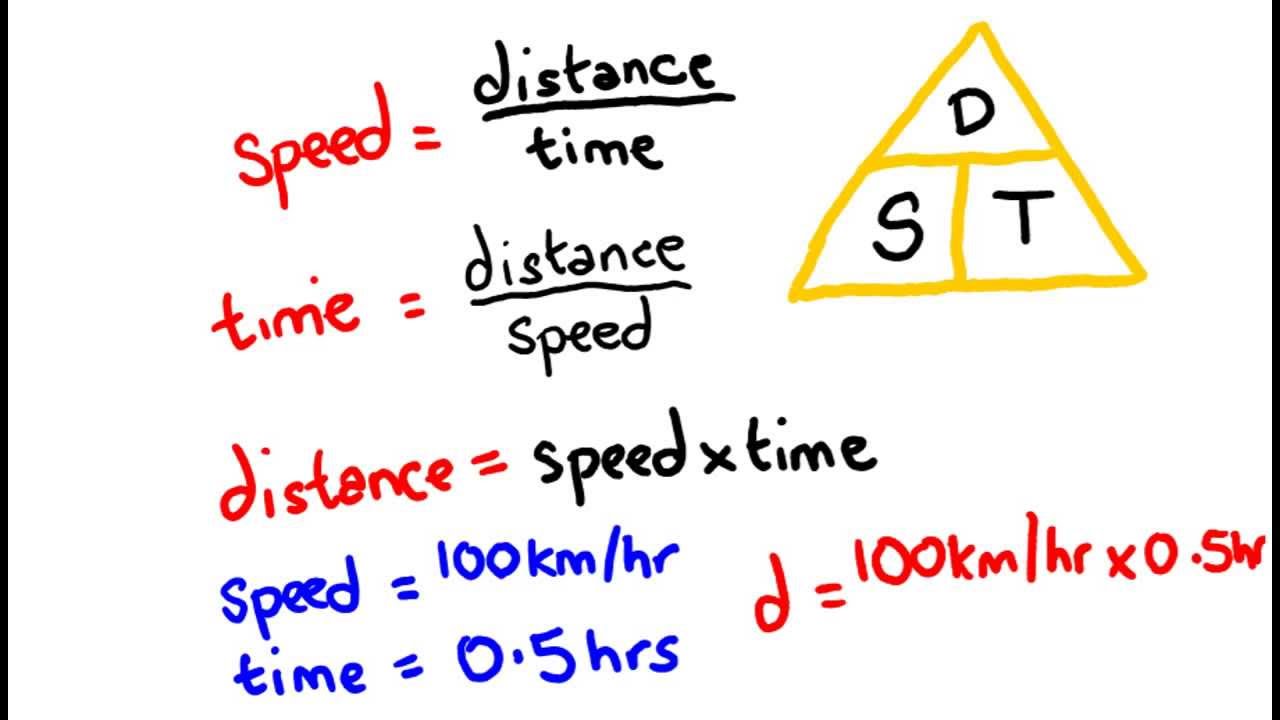
The initial velocity (vi) is the velocity of the object before a change due to acceleration. On the other side, the final velocity is the speed (along with direction) of the same moving object once it has reached its final position. Initial velocity is the speed (along with direction) of the object with which it starts moving. Some of the units in which one can express velocity is miles per hour (mph), kilometres per second (km/s), and kilometres per hour (kph). T is the time the object took to complete the movementĪlthough the SI unit for velocity is m/s (meter per second), it can be expressed in any unit of d/t (distance per time).

R is the rate (sometimes denoted as v, representing velocity) A simple formula given below is the most common and easiest way to calculate velocity. For instance, if an object travels towards the west at 5 meters per second (m/s), then its velocity will be 5 m/s to the west. Hence, to determine the velocity as per this definition, we should be familiar with both the magnitude and direction. Velocity is a vector measurement of the rate of motion of an object and the direction in which it is moving. Here, we will be going to discuss this concept in detail. Considering such difficulties and thus eliminating them, our scientists came up with the concept of velocity to help the observers in identifying the faster or slower objects with ease. However, determining the faster object is quite difficult if the two are travelling in opposite directions. Identifying which of the two objects is moving faster than the other one is easy if they both are moving in the same direction. Let’s take an example where two objects are moving. It is what tells how slow or fast something is moving. In simple words, the term velocity gives us an idea of the speed at which an object is moving in a particular direction. To be specific, the velocity of an object can also be defined as the rate of change in the object’s position corresponding to a frame of reference and time. The importance of knowing the limits of models is discussed and some of the limits of this model are pointed out.Velocity in physics is defined as a vector measurement of the direction and rate of the motion.
The physics here is also applicable to jumps in other sports including skiing and mountain biking. Thus we are able to explain with a relatively simple model why a snowboarder may jump from rather high ledges and land comfortably. A judicious choice of the geometry of the jump leads to a force on landing that is equal to the force that the snowboarder would feel if they were standing at the landing point independent of the height from which the snowboarder jumps. It is shown that the flexing of the legs, the softness of the snow, the angle of the landing surface and the forward motion of the snowboarder can contribute significantly to reducing the force on landing. We further use our numerical results to evaluate how these two variables relate to the effects of air resistance for balls dropped from varying heights.Īn application of Newton's second law to a snowboarder dropping off a vertical ledge shows that the average normal force during landing (force exerted by the ground on the snowboarder) is determined by four factors. We do this by summarising the results of a set of numerical simulations of various balls falling under the effects of both gravity and air resistance by means of a carefully chosen graph: a plot of an object's cross-sectional surface are versus its mass. In this paper we develop a graphical tool intended to make this step as simple and effective as possible.
#VELOCITY PHYSICS FREE#
Taking the additional step of clarifying when it is reasonable to ignore air resistance makes students' reconciliation of their everyday experiences with the physics principle of free fall more likely. However, this step is rarely, if ever, provided with justification in undergraduate texts, leading students to believe that what they are taught does not apply to their everyday experience. Mathematically, ignoring the effect of air resistance is crucial, however, since it renders such problems tractable. To a student, this assumption disconnects from their everyday experience. An important instance of this occurs when students are instructed to ignore the effect of air resistance when solving kinematics problems. This is especially true when they perceive a principle taught in physics class as being in conflict with their experience. Many students find it difficult to apply certain physics concepts to their daily lives.


 0 kommentar(er)
0 kommentar(er)
